math

HISTORY of MATH

$archemedes$

Mathematics is an evolving discipline. It is constantly expanding and changing. Although the ancient Greeks, for instance, began to develop number theory and made major contributions to geometry and logic, they had little inkling of probability, which wasn't formalized until the mid 1600s.

$greek math$

Following is a brief history of mathematics, according to topic and mathematician. Note that most dates are approximations as these individuals often worked years in furthering mathematics. Also, because so many people have contributed to mathematics throughout history, this list is quite subjective and we picked who we feel are some of the most significant contributors. Undoubtedly, you will be able to name several others that should be included here.

$world of math$

3,000 B.C.E.	Egyptians and Babylonians begin the development of number systems and early bookkeeping. Simple problems of arithmetic and geometry necessary to a civilized society become commonplace.	$babylonian numbers$ $babylonian numbers$ $egyptian numbers$
700 B.C.E.	Ancient Greece starts to flourish. Greek thinkers contribute number theory, geometry, and logic to mathematics.	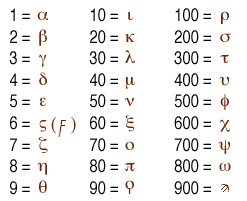$greek numbers$
530 B.C.E.	Pythagoras, one of the most famous of the Greek mathematicians and philosophers, founds the Pythagorean movement.	$pythagorus$ $pythagorean$
300 B.C.E.	Euclid completes his writing of Elements, 13 volumes on mathematics.	$euclid$ $Euclid The Elements$
100 C.E.	Astronomers begin to develop trigonometry.	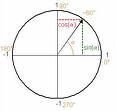$trigonometry.$
170 C.E.	Ptolemy, mathematician and astronomer, declares that the earth is the center of the universe. This becomes the dominate view until the 17th century when Copernicus claims that the sun is the center of the solar system.	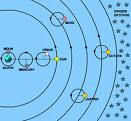$Ptolemy$ $Ptolemy$
200 C.E.	Diophantus, a Greek mathematician, develops algebra. He is considered by many to be the father of that subject.	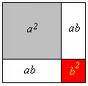$Diophantus$ $Diophantus$
540 C.E.	Diophantus and astronomer, advances mathematics by solving the quadratic equation.	$quadratic equation$ $quadratic equation$
600 C.E.	Geometry, algebra, and numeral systems benefit from Hindu and Arabian thought. The idea of zero is introduced	$Hindu$ $Hindu zero$
775 C.E.	The translation of Hindu mathematics to Arabic takes place.	$Arabic hindu numbers$
830 C.E.	al-Khowarizml, an Arabian, works with algebra, numeral systems, and equations.
1100 C.E	Arabic and Hindu mathematics spread throughout Western Europe.	$Arabic and Hindu mathematics$
1200 C.E.	Leonardo of Pis a (Fibonacci), an Italian, works with equations, sequences, series, and Pi.	. $Fibonacci$ $Fibonacci$
1478 C.E.	The first mathematics books are printed.	$first mathematics books$
1489 C.E.	The signs of + and - are introduced	$+ and - are introduced$
1500 C.E	Negative numbers and perspective are introduced.	$Negative numbers$
1525 C.E.	Great work is done on solving equations.	$solving equations$
1540 C.E.	Imaginary numbers are explored.	$Imaginary numbers$
1557 C.E.	Englishman Robert Record writes the first English algebra text.	$Englishman Robert Record$
1560 C.E.	The Italian Girolamo Cardano works with complex numbers, equations, and probability.	$Girolamo Cardano$
1580 C.D.	Decimals are introduced.	$Decimals$ $Decimals$
1614 C.D.	John Napier, Scottish mathematician, creates the first system of logarithms. He is the first to use the decimal point.	$John Napier$ $John Napierbook$ $John Napier logorhythms$
1630 C.E.	The coordinate system is developed.	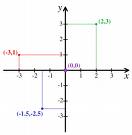$coordinate system$
1640 C.D.	Rene Descartes, French philosopher, scientist, and mathematician, works on systemizing analytic geometry. He also attempts to classify curves according to the types of equations that produce them.	$Rene Descartes$ $Rene Descartes$
1645 C.D.	Pierre de Fermat, French mathematician, studies various topics, including coordinates, polygons, probability, and the Pythagorean theorem.	$Pierre de Fermat$ $Pierre de Fermat$
1650 C.D.	Blaise Pascal, French philosopher, physicist, and mathematician, formulates one of the basic theorems of projective geometry, known as Pascal's theorem. He also invents the first adding machine.	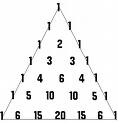$Blaise Pascal$ $Blaise Pascal$ $Blaise Pascal$
1680 C.E.	The German Gottfried Wilhelm von Leibniz works on calculus, functions, and infinity.	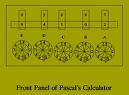$Gottfried Wilhelm von Leibniz$ $Gottfried Wilhelm von Leibniz$ $Gottfried Wilhelm von Leibniz$
1700 C.E.	Work on determinants is done.	$determinants$
1780 C.D.	Complex numbers are explored by several mathematicians.	$abraham molrie$ $complex numbers$ $complex numbers$
1799 C.E.	The Metric System is introduced.	$metric system$ $metric system$
1800 C.E.	Theories on projection are developed. Number theory is explored.	$Theories on projection$
1810 C.E.	Carl Friedrich Gauss, a German mathematician, expands the study of number theory.	$Carl Friedrich Gauss$ $Carl Friedrich Gauss$ $Carl Friedrich Gauss$
1820 C.E.	The Russian Nikolai Ivanovich LCl'Qachevsky works on geometry.	$Nikolai Ivanovich$ $Nikolai Ivanovich$
1840 C.E.	Various mathematicians work with matrices, vectors, and symbolic logic.	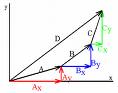$matrices$ $vectors$ $boole$ $symbolic logic$
1870 C.E.	George Cantor works with infinite sets.	$George Cantor$ $George Cantor$
1905 C.E.	Albert Einstein develops the theory of relativity.	$Albert Einstein$ $Albert Einstein$
1910 C.E.	Various mathematicians, including Alfred North Whitehead and Bertrand Russell, study the logical foundations of mathematics.	$alphred whitehead$ $bertrand russell$ $logical foundations of mathematics$
1920 C.E.	Emmy Noether studies abstract algebra.	$Emmy Noether$ $abstract algebra$
1945 C.E.	Various mathematicians and researchers work on computers.	$researchers work on computers$ $otto$
1976 C.E.	Kenneth Appel and Wolfgang Haken find a solution of the Four Color Problem.	$Kenneth Appel$ $Wolfgang Haken$ $four color problem$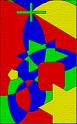
1977 C.E.	Robert Connelly finds a rigidity counterexample.	$Robert Connelly$ $Robert Connelly$
1993 C.E.	Andrew Wiles presents what he believes is the proof of the most famous problem in mathematics-Fermat's last theorem. At the time of this book's printing, Wiles' work has not been confirmed.	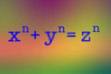$andrew wiles$ $Fermat's last theorem$ $Fermat's last theorem$